Project Outline
Detailed ideas and development records
The description on the home page of the Emergent Language project page gives an overview of the motivation and directions of this project. This page contains additional details on key theoretical advancements and results we have obtained.
Table of Contents
Overarching Goal
We want to create a deep learning system attempting to solve a task from which a ‘language’ that demonstrate properties of human language emerges.
Why do we want to do this?
Such an emergent language is grounded in the model’s actual understanding of the task and the semantics involved, and doesn’t just rely upon syntactic dependencies. That is, it demonstrates groundedness.

Properties of Language
This section describes various properties of language we hope to see demonstrated by the created synthetic language. The first three ({discrete, sequential, variable-length}) are explicitly built into the design of the architecture, the remainder are metrics that may have auxiliary or indirect effect on the model.
Discrete
Language is represented and understood in discrete symbols. An emergent language should possess properties of discreteness/quantization, as opposed to working with traditional real-valued vectors. The most explicit form of discreteness is generating language in one-hot form: the token in the vocabulary with the highest probability is selected at each time step. However, other acceptable forms of discreteness include Vector-Quantized Variational Autoencoder (VQ-VAE)-style mechanisms, in which continuous vectors are ‘snapped’ to the closest embedding in a limited and trainable set of embeddings. This can be interpreted as directly associating tokens with an embedding.
Sequential
Language is inherently ordered and temporal. Thus, it must possess an intrinsic ordering - as opposed to a standard vector which is mapped to and from in a dense, fully-connected way. A language is sequential if the processes by which it is generated recognize temporality: for instance, generation and interpretation via recurrent or transformer-like methods. However, being sequential does not mean that the specific order is rigid/static. In English, larger sequences of tokens can be rearranged with minimal modification to semantics. (Larger seuences of tokens can be rearranged with minimal modification to semantics in English.) In fact, we hope to see evidence of similar behavior in an emergent language - low-level rigid ordering (the building blocks of syntax) with high-level interchangeability of semantic expression.
Variable-Length
Grounded
Large language models trained to model human language data learn sophisticated syntactic relationships between symbols, to the point of being able to perform seemingly complex operations with language. However, these models’ lack of robustness has been well documented, and stems from a fundamental flaw within language models: lack of groundedness. That is, a language model may know the meaning of a token and its complex relationships with other tokens, but its understanding is restricted to the syntactic level of language. On the other hand, humans have a deeper semantic understanding of language. Language is a reference, rather than an ends, to understand semantics. A primary goal of this project is to observe robustness in an emergent language stemming from groundedness.
Groundedness is an abstract concept, but fundamentally it must demonstrate that the language’s tokens are fundamentally rooted in the semantic rather than the syntactic level. This can be assessed by testing the relationship between tokens and the underlying semantic objects, for instance by perturbing the representation in ways that shouldn’t affect the semantics and measuring the change in language activity.
Compositional
Hockett’s Design Features
View complete descriptions here
Clearly irrelevant features have been ommitted.
| Feature | Relevance |
|---|---|
| Interchangeability | Comes with the model; the model should be capable of generating every possible sequence. Language is accessible to all models. |
| Total Feedback | Recurrent models demonstrate this property. Models like the DLSM explicitly builds this listening-speaking design into the architecture. |
| Semanticity | This is a part of groundedness. |
| Arbitrariness | This is built into the experiment design; the language is initialized randomly and therefore emergence of symbols is arbitrary. |
| Discreteness | The discreteness itself is built into the expreriment design; that is, a limited set of vectors/tokens are accessible to construct the language. Additionally, the language should demonstrate the presence of a discrete syntax. |
| Displacement | This is perhaps a part of abstraction, but is not relevant to the current task scope. This may be demonstrable in a reinforcement learning context. |
| Productivity | The ability to develop essential attributes that can be combined in meaningful ways to form novel utterances (e.g. trained on all combinations of shapes except for green triangle, but is able to represent green triangle by virtue of having experience with green things and triangle things). |
Note: a lot of the features that were ommitted likely would have been modelable/demonstrable by an RL environment project.
Tasks
Autoencoding with Language Latent Space
Intuitively, we can understand the task of communication as one of autoencoding - one agent (an encoder) collaborates with another agent (a decoder) to structure the latent space such that information can reliably be encoded into it and decoded out of it. Lan et al. say as much in their paper “On the Spontaneous Emergence of Discrete and Compositional Signals”.
In autoencoding task, the desired output is identical to the output. The decoder’s objective is to perfectly reconstruct the input given a language-like latent representation. This language-like representation must satisfy at least some of the axioms of language (discussed more in-depth in the Properties of Language section). For the duration of our work on this task, we used a latent space satisfying two of the three core properties - discrete/symbolic and sequential. The intuition is that the encoder and decoder must collaboratively develop an understanding of core features in the image and represent it in important word-like tokens arranged in a meaningful language-like sequence.
Empirically, we observe good performance on the MNIST dataset with a sufficiently large vocabulary size and sequence length.
A static demonstration of autoencoder reconstructive capabilities and internal + quantized language/’communication’.

A dynamic demonstration of autoencoder reconstructive capabilities along the temporal/sequential language/’communication’ axis.
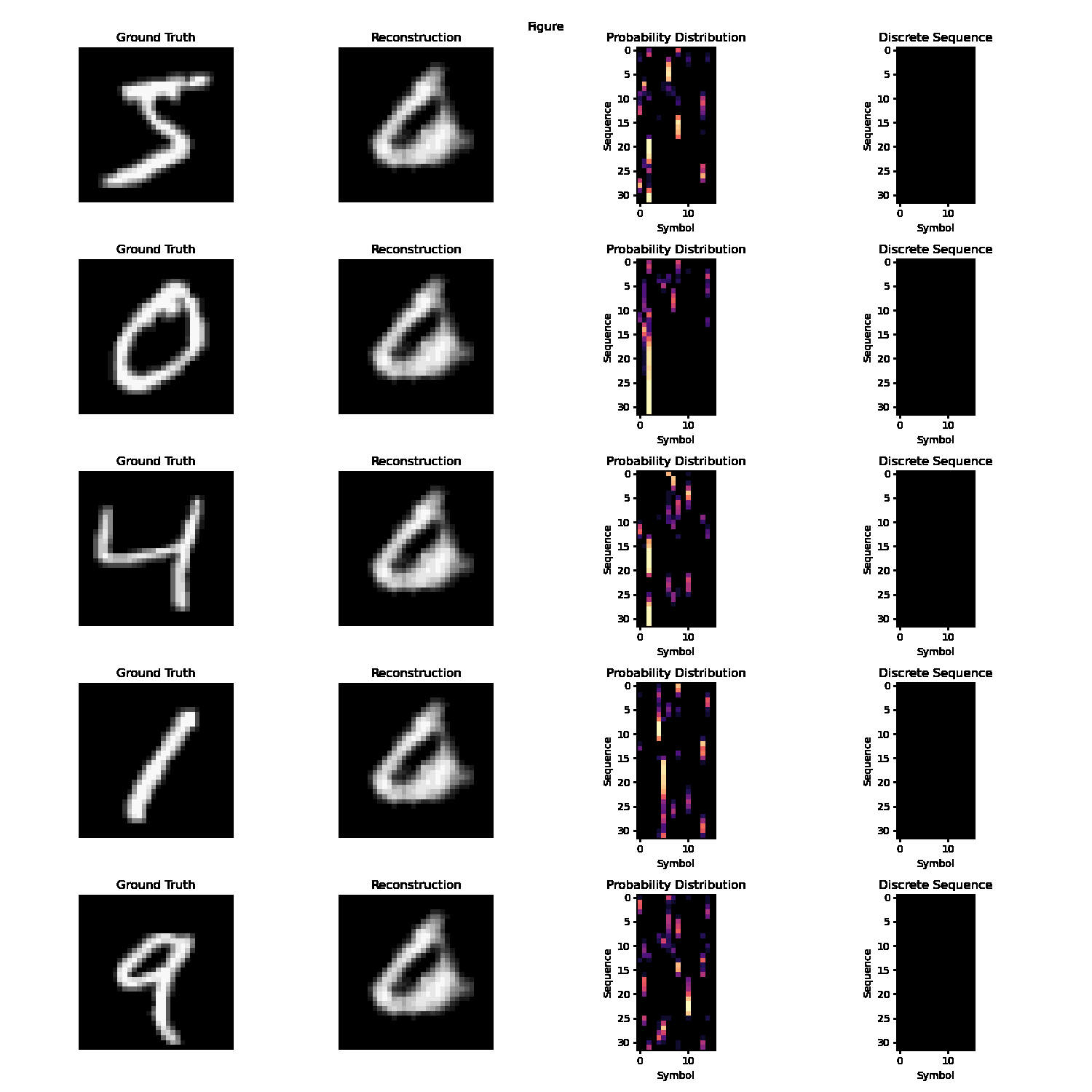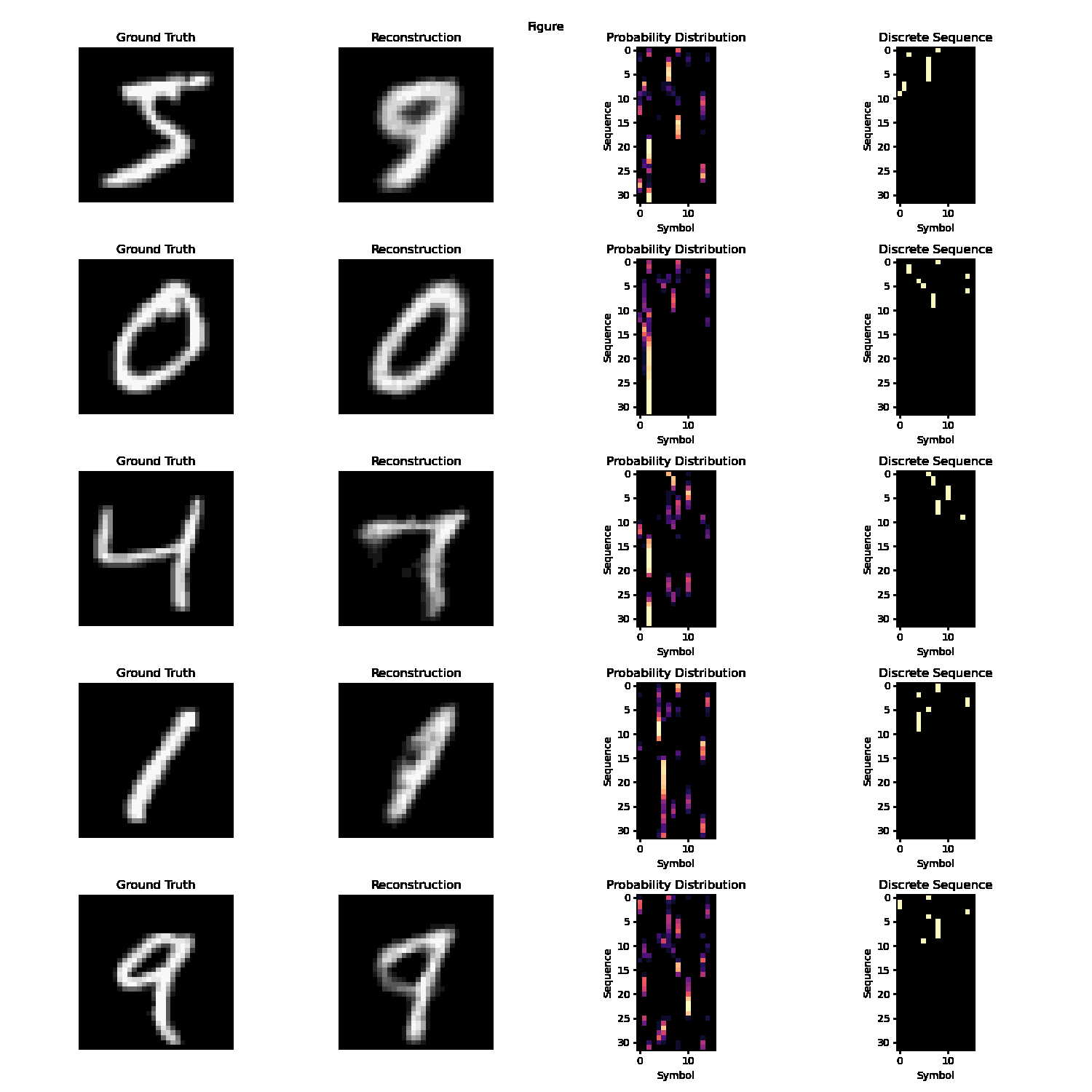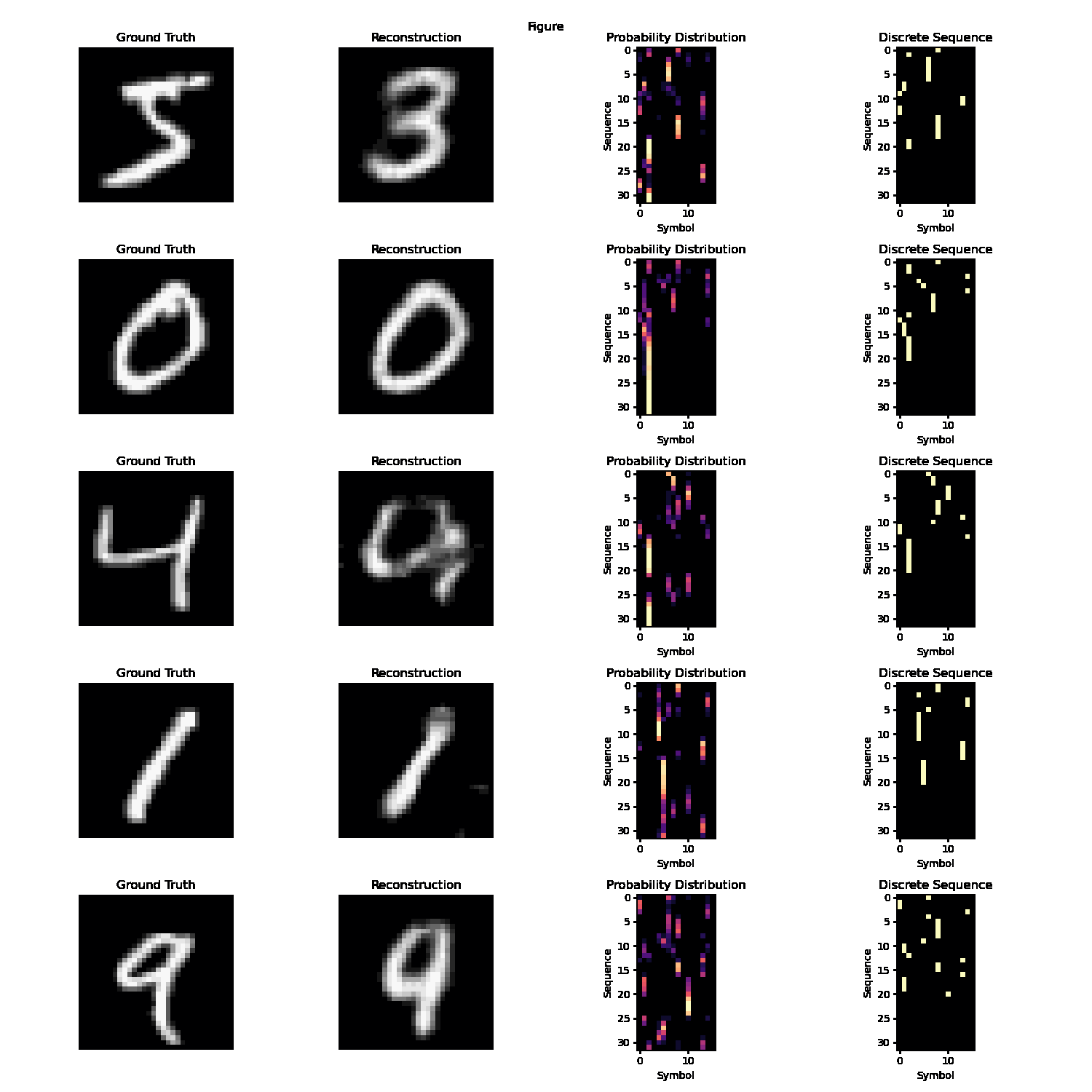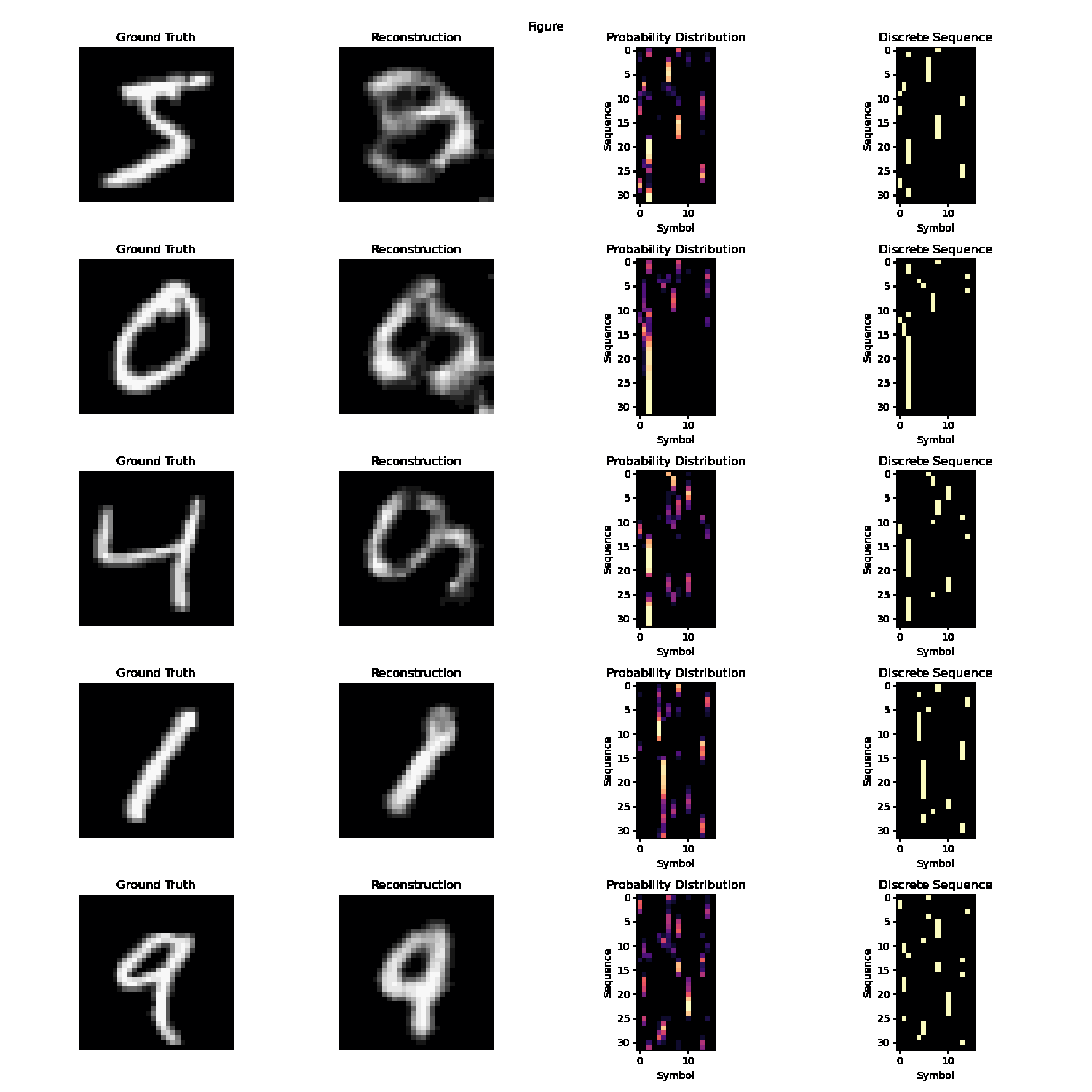
However, the task of autoencoding with a language latent space becomes practically and philosophically dubious for any dataset more complex than MNIST, like CIFAR-10/100, ImageNet, or a semantic subset like the Stanford Dogs and Cats dataset. There really are only perhaps twenty or less actual digit forms; all remaining digits closely conform to one of these digit forms, since the dataset is low-resolution, centered, and grayscale. A network can reliably autoencode MNIST just be learning these digit form ‘templates’. However, for more complex datasets, autoencoding as a task for emergent language becomes philosophically problematic. The purpose of language is not to encode information in a way that optimizes for minimum information loss; rather, it is inherently abstract. However, autoencoding rewards the development of explicit structures and information systems, which is in fact antithetical to the purpose of the project.
VQ-AE-GAN
The VQ-AE-GAN (Vector-Quantized Autoencoder Generative-Adversarial-Network) system is an attempt to build a task that rewards abstractness by fitting the vector-quantized (i.e. discrete, language-like latent space) autoencoder into a Generative Adversarial Network system. In a traditional GAN system, the generator generates images and the discriminator classifies whether an input was pulled from the dataset or generated by the generator. The generator’s goal is to fool the discriminator by maximizing its loss; the discriminator’s goal is to minimize its loss. Such an ‘adversarial’ relationship leads to the development of realstic images that are sophisticated because they demonstrate abstract properties also present in real/true images.
If we replace the generator with a vector-quantized autoencoder (i.e. the same autoencoder architecture used for the previous task), then the vector-quantized autoencoder does not necessarily need to reconstruct the exact input pixel-for-pixel, but rather just develop a reconstruction that seems realistic to a discriminator. The discriminator is an entity that theoretically is capable of rewarding abstraction. To provide additional information to the discriminator as to force the generator to avoid trivial solutions, embeddings for each reconstruction are obtained form an auxiliary feed-forward neural network that are also passed (along with the reconstruction) into the discriminator for generated-or-real classification.
We have not seen much success with this approach.
Object-Based Geometric Scene Similarity
Heavily inspired by Choi et al.’s paper “Compositional Observer Communication Learning from Raw Visual Input”, the geometric scene similarity task is the most successful one to date, both philosophically and pragmatically. The model observes two geometric scenes and must determine whether they represent the same set of objects or not. Each geometric scene is comprised of a certain number of objects; each object is a certain color and a certain shape. Two scenes are considered the same if there is a one-to-one correspondence between a unique color-shape combination between both images.
Metrics
This section outlines the standardized experiment conditions and metrics for which we are pursuing model development for this task.
To measure the model’s understanding of this task, we use three metrics under Alec mode. In Alec mode, each scene is comprised only of the number of objects, the color of all the objects, and the shape of all the objects. For instance, we may have three red squares or one blue circle, but never multiple shapes of different types. The purpose of Alec mode is to allow the scene to be decomposed into three essential attributes, whereas a generic task becomes more of a brute listing task.
We hold out one combination of shapes (arbitarily, we have settled upon red squares). The model is trained on all combinations of color and shape, with between 1 and 3 objects in each scene (inclusive), except for red squares. This means that the model sees red shapes (red circle, red triangle) and square objects (blue square, green square) but not the specific combination of red and square. This set constitutes the in-distribution set - this is what the model is exposed to and trained on. The in-distribution accuracy (abbreviated as ID accuracy) is simply the accuracy the model incurs on this in-distribution dataset.
A sample of the in-distribution dataset.

The out-of-distribution dataset (OOD) comprises of scene pairs in which at least one of the scenes features out-of-distribution shapes. The purpose of this dataset is to evaluate the performance of the model on novel combinations of abstract features that it has not been trained on before. The out-of-distribution accuracy (abbreviated as OOD accuracy) is the accuracy of the model on this OOD dataset. To generate the out-of-distribution dataset, use the following algorithm:
1. Randomly select whether the target label should be 1 (two scenes are the same) or 0 (two scenes are different) with equal probability.
2. If the target label is 1:
a. Select a set of OOD shapes.
b. Generate two scenes using the same OOD shapes.
3. If the target label is 0:
a. Select a set of OOD shapes.
b. Select a set of shapes, ID or OOD, that is different from the set chosen in 3a.
c. Generate two scenes using the sets in 3a and 3b.
[Graphs forthcoming]
The out-of-distribution color-spec accuracy (abbreviated as OOD CS accuracy) is the model performance on a slightly modified OOD dataset, in which inputs with a label of 0 (i.e. the two scenes are different) must all be of the same color. This prevents the model from easily exploiting color to perform well on OOD contxexts in which two scenes are different. To generate the OOD CS dataset, use the following algorithm:
1. Randomly select whether the target label should be 1 (two scenes are the same) or 0 (two scenes are different) with equal probability.
2. If the target label is 1:
a. Select a set of OOD shapes.
b. Generate two scenes using the same OOD shapes.
3. If the target label is 0:
a. Select a set of OOD shapes.
b. Select a set of shapes, ID or OOD, that is different from the set chosen in 3a but which has the same color as the set of shapes in 3a.
c. Generate two scenes using the sets in 3a and 3b.
[Graphs forthcoming]
Relation-Based Geometric Scene Similarity
A more complex task is to incorporate relationships between objects into the visual representation of the scene. Philosophically and linguistically, the scenes in object-based geometric scene similarity only semantically contain nouns and adjectives. However, verbs are relationships and enable more complex interactions and formulations of language, as verbs are explicitly compositional. In a relation-based geometric scene similarity task, a scene is comprised not only of a set of objects, but a set of objects and relationships between them. For instance, some objects reside within other objects and lines (unidirectional, bidirectional, or adirectional) connecting different objects. For two scenes to be the same, not only must the same objects be present, but the relationships between them must be retained. This requires a formulation of relationships.
Movement Scene Similarity
Models
Dual Listener-Speaker Model
Standard DLSM:

DLSM with Variable-Length Mechanism:
